DERIVADA DE UNA FUNCIÓN
La derivada es uno de los conceptos de significado dialéctico en matemáticas. La derivada, en el caso de una función real de una variable real, es el resultado de un límite y representa, geométricamente, la pendiente de la recta
tangente a la gráfica de la función en un punto. En la Física,
la derivada se puede entender como la
velocidad instantánea. Se puede considerar la derivada
como la razón de variación de una masa poblacional
respecto de la variación del tiempo.
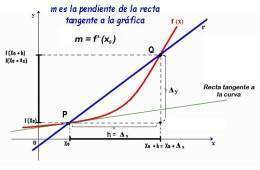
Se llama derivada de la función y = f(x) en el punto x0 y se denota por f’(x) al límite de la razón
TÉCNICAS DE DERIVACIÓN
- DERIVACIÓN DE FUNCIONES ALGEBRAICAS
Generalmente la derivación se lleva acabo aplicando fórmulas obtenidas mediante la regla general de la derivación y que calcularemos a continuación, de estas podemos derivar las funciones algebraicas, trascendentales, sucesivas y combinadas.
Derivada de una función de grado (n)
Una función de grado n, donde n es un entero positivo, se representa por 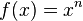
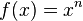
y su derivada es  .
.
Cabe hablar de la derivada de una función potencial de exponente real sin mencionar grado. Por ejemplo 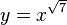
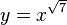
que es más fácil considerando
Algunos tipos de este tipo de funciones son: Función cuadrática, función cúbica, entre otras.
Pasos para cada tipo de derivación
1. Constantes- En este caso todas las derivadas de una constante son iguales a cero.
2. Función identidad- cualquier variable como a, b, c su derivada es 1. f(x)= entonces f'(x)=1
3. Regla de las potencias- Si se tiene un termino que esta elevado a una potencia en una función
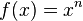
Formula: 
4. Regla del factor constante- 1.Se deriva la x con la regla de las potencias. 2.Se multiplica el resultado por la constante (el número normal) Fórmula: f ‘(x)=(a)nxn-1
5. Regla de la suma- Se deriva con las reglas anteriores a cada termino de la función. Si F(x)=g(x)+f(x) entonces F’(x)=g ‘(x)+f ‘(x)
6. Regla de la diferencia- Se realizan los mismos pasos que en la regla de la suma igual pero restando.
7. Regla del producto- 1.Identificar las dos funciones, 2.Multiplicar la primera (u) por la derivada de la segunda (v), y se suma el producto de la segunda por la derivada de la primera. Formula: f ‘(x)=uv’+vu’
8. Regla de la derivada del cociente- 1.Identificar las dos funciones u y v, 2.Multiplicar la derivada de la primera (u) por la segunda (v), y se resta el producto de la primera por la derivada de la segunda, 3. Dividir todo entre la segunda al cuadrado. Formula: f ’(x)=vu’-v’u/v^2
REGLA DE LA CADENA
es una fórmula para calcular la derivada de la composición de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la función compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)]
es:
o escrito en notación de Leibniz
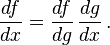
Derivadas de funciones logarítmicas y exponenciales
Lo anterior es válido para todo c, pero para c < 0 el resultado es un número complejo.Lo anterior es válido para todo c, pero para c < 0 el resultado es un número complejo.
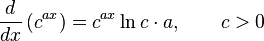
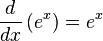
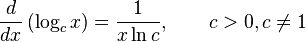


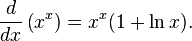
No hay comentarios:
Publicar un comentario