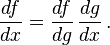CALCULO INTEGRAL : 2016

INTEGRAL DEFINIDA

MAPA MENTAL

UN PROBLEMA DE APLICACIÓN RELACIONADO CON

LA ECONOMÍA

Se espera que la compra de una nueva máquina genere un ahorro en los costos de operación. Cuando la máquina tenga x años de uso la razón de ahorro sea de f(x) pesos al año donde f(x) = 1000 + 5000x.

a) ¿Cuánto se ahorra en costos de operación durante los primeros seis años?

b) Si la máquina se compró a $ 67500 ¿cuánto tiempo tardará la máquina en pagarse por sí sola?

a) Para conseguir el ahorro durante los primeros seis años calculamos

Al cabo de seis años el ahorro asciende de $ 96000

b) Dado que el precio de compra es de $ 67500, el número de años de uso que se requieren para que la máquina se pague sola es n, entonces

1000n + 2500 n² = 67500 Þ 2500 n² + 1000n - 67500 = 0

5 n² + 2n - 135 = 0

Hallamos los valores de n aplicando la resolvente y resulta n₁ = -5,4 (imposible para nuestro problema) y además n₂ = 5.

Se tardarán 5 años para que la máquina se pague sola.

INTEGRAL INDEFINIDA

En cálculo infinitesimal, la función primitiva o anti derivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.

Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.

Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F₁ y F₂ son dos primitivas de f, entonces existe un número real C, tal que F₁ = F₂ + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa como:

El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.

EJEMPLO:

Una primitiva de la función f(x)= cos(x) en R es la función f(x)= sin(x) ya que:

Dado que la derivada de una constante es cero, tendremos que cos(x) tendrá un número infinito de primitivas tales como sin(x), sin(x) + 5, sin(x) - 100, etc. Es más, cualquier primitiva de la función f(x) = cos(x) será de la forma

sin(x) + C

donde C es una constante conocida como constante de integración.

CONSTANTE DE INTEGRACIÓN

La derivada de cualquier función constante es cero. Una vez que se ha encontrado una primitiva F, si se le suma o resta una constante C, se obtiene otra primitiva. Esto ocurre porque :

(F + C) ' = F ' + C ' = F ' + 0 = F '. La constante es una manera de expresar que cada función tiene un número infinito de primitivas diferentes.

Para interpretar el significado de la constante de integración se puede observar el hecho de que la función f (x) es la derivada de otra función F (x), es decir, que para cada valor de x, f (x) le asigna la pendiente de F (x). Si se dibuja en cada punto (x, y) del plano cartesiano un pequeño segmento con pendiente f (x), se obtiene un campo vectorial como el que se representa en la figura de la derecha. Entonces el problema de encontrar una función F (x) tal que su derivada sea la función f (x) se convierte en el problema de encontrar una función de la gráfica de la cual, en todos los puntos sea tangente a los vectores del campo. En la figura de la derecha se observa como al variar la constante de integración se obtienen diversas funciones que cumplen esta condición y son traslaciones verticales unas de otras.

PROPIEDADES

-Linealidad de la integral indefinida

La primitiva es lineal, es decir:

1. Si f es una función que admite una primitiva F sobre un intervalo I, entonces para todo real k, una primitiva de kf sobre el intervalo I es kF.

2. Si F y G son primitivas respectivas de dos funciones f y g, entonces una primitiva de f + g es F + G.

La linealidad se puede expresar como sigue:

-La primitiva de una función impar es siempre par

En efecto, como se ve en la figura siguiente, las áreas antes y después de cero son opuestas, lo que implica que la integral entre -a y a es nula, lo que se escribe así: F(a) - F(-a) = 0, F siendo una primitiva de f, impar. Por lo tanto siempre tenemos F(-a) = F(a): F es par.

-La primitiva F de una función f par es impar con tal de imponerse F(0) = 0

En efecto, según la figura, las áreas antes y después de cero son iguales, lo que se escribe con la siguiente igualdad de integrales:

Es decir F(0) - F(-a) = F(a) - F(0). Si F(0) =

0, F(-a) = - F(a): F es impar.

-La primitiva de una función periódica es la suma de una función lineal y de una función periódica:

Para probarlo, hay que constatar que el área bajo una curva de una función periódica, entre las abcisas x y x + T (T es el período) es constante es decir no depende de x. La figura siguiente muestra tres áreas iguales. Se puede mostrar utilizando la periodicidad y la relación de Chasles, o sencillamente ¡con unas tijeras! (cortando y superponiendo las áreas de color).

En término de primitiva, significa que F(x + T) - F(x) es una constante, que se puede llamar A.

Entonces la función G(x) = F(x) - Ax/T es periódica de período T. En efecto

G(x +T) = F(x + T) - A(x + T)/T = F(x) + A - Ax/T - AT/T = F(x) - Ax/T = G(x).

Por consiguiente

F(x) = G(x) + Ax/T

es la suma de G, periódica, y de Ax/T, lineal.

UND 1. DERIVADA DE UNA FUNCIÓN Y TÉCNICAS DE DERIVACIÓN

DERIVADA DE UNA FUNCIÓN

La derivada es uno de los conceptos de significado dialéctico en matemáticas. La derivada, en el caso de una función real de una variable real, es el resultado de un límite y representa, geométricamente, la pendiente de la recta

tangente a la gráfica de la función en un punto. En la Física,

la derivada se puede entender como la

velocidad instantánea. Se puede considerar la derivada

como la razón de variación de una masa poblacional

respecto de la variación del tiempo.

Se llama derivada de la función y = f(x) en el punto x0 y se denota por f’(x) al límite de la razón

es decir:

TÉCNICAS DE DERIVACIÓN

DERIVACIÓN DE FUNCIONES ALGEBRAICAS

Generalmente la derivación se lleva acabo aplicando fórmulas obtenidas mediante la regla general de la derivación y que calcularemos a continuación, de estas podemos derivar las funciones algebraicas, trascendentales, sucesivas y combinadas.

Derivada de una función de grado (n)

Una función de grado n, donde n es un entero positivo, se representa por

f(x)=x^{n}

y su derivada es

f'(x)=nx^{n-1}

Cabe hablar de la derivada de una función potencial de exponente real sin mencionar grado. Por ejemplo

y = x^{\sqrt{7}}

que es más fácil considerando

ln y = \sqrt{7} ln x

Algunos tipos de este tipo de funciones son: Función cuadrática, función cúbica, entre otras.

Pasos para cada tipo de derivación

1. Constantes- En este caso todas las derivadas de una constante son iguales a cero.

2. Función identidad- cualquier variable como a, b, c su derivada es 1. f(x)= entonces f'(x)=1

3. Regla de las potencias- Si se tiene un termino que esta elevado a una potencia en una función

f(x)=x^{n}

Formula:

f'(x)=nx^{n-1}

4. Regla del factor constante- 1.Se deriva la x con la regla de las potencias. 2.Se multiplica el resultado por la constante (el número normal) Fórmula: f ‘(x)=(a)nxn-1

f'(x)=(a)nx^{n-1}

5. Regla de la suma- Se deriva con las reglas anteriores a cada termino de la función. Si F(x)=g(x)+f(x) entonces F’(x)=g ‘(x)+f ‘(x)

6. Regla de la diferencia- Se realizan los mismos pasos que en la regla de la suma igual pero restando.

7. Regla del producto- 1.Identificar las dos funciones, 2.Multiplicar la primera (u) por la derivada de la segunda (v), y se suma el producto de la segunda por la derivada de la primera. Formula: f ‘(x)=uv’+vu’

8. Regla de la derivada del cociente- 1.Identificar las dos funciones u y v, 2.Multiplicar la derivada de la primera (u) por la segunda (v), y se resta el producto de la primera por la derivada de la segunda, 3. Dividir todo entre la segunda al cuadrado. Formula: f ’(x)=vu’-v’u/v^2

REGLA DE LA CADENA

es una fórmula para calcular la derivada de la composición de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la función compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)]

es: